ラモン・イ・カハル自伝
「ラモン・イ・カハル自伝 ―悪童から探求者へ (小鹿原健二訳、萬年甫解説、後藤素規編、里文出版)」を読み終えました。
カハールについては、このブログでも何度か取り上げました。「ニューロン説」を唱え、ノーベル賞を受賞した歴史的科学者です。
神経学の源流 2 ラモニ・カハール
脳の探求者ラモニ・カハール スペインの輝ける星
「ラモン・イ・カハル自伝」は、カハールが悪童として名を馳せた少年期から、学問を志すようになった頃までを綴った自伝です。カハールがかなりの悪童であったことは事実ですが、彼がハチャメチャな行動を行うに至った内面の描写が面白く、まるで良質の冒険小説を読んでいるようでした。一方で、彼は凄く分析的に周囲のことを観察できる子供だったようです。教師を客観的に分析し、何故その教師の授業を聞く気にならなかったかも記しています。他面、カハールには試験での遅刻癖があり、再三失敗したということも、記されていました。色々と規格外の人物だったのですね。
本書には、教訓的な表現が多く出てきて、なかなか含蓄があります。
その経験とは、様々な似たような事態にもあてはまるが、次の極めてありふれた格言「困難な仕事において、勝利をおさめようと思うなら、充分な時間と労力をかけて、明らかに必要なものを予め身に備えながら、仕事に打ち込め」の中に含まれていた。結局、努力は、決して害にならず、むしろ、別の機会に役立った。それにひきかえ、努力の不足は、それがわずかであっても、惨めな失敗をもたらすのである。
何か有益な教訓を生み出さないような「愚かな行動」はないものだ。
アマチュアの絵書きが大体そうであるように、私は基本的な色調をよく識別した。しかし、灰色の使い方の難しさを知らなかったし、また、「自然は、単純な色を示すことはほとんどない」ということに全く無知だった。
聴覚と同様に、風景の色彩感覚において、いろいろな組み合わせしか存在しない」ということは知られている。色彩には色々の割合で、常に、白と黒―聴覚における無音と有音に相応する―が混じり合っている。色彩に関するこのような認識が子供に欠けていることは止むを得なかった。そんな事を知らずに、私は、色彩を単純化し、図式化した。ハーモニーを無視してメロディーだけを表現するヘボ楽士のように、未熟な絵書きは、主要な色調だけを描く。ここで街頭絵書きの気違いじみた色付けを思い出さない人はいないだろう。(略)
私も経験のなさから、このような嘆かわしい欠陥に犯されていた。しかし、暗中模索している中に、私はこの欠陥の一部を克服して、調和のとれた色調を見分けることができるようになった。例えば、それまで、あらゆる緑色を単純に芝生のような純粋な緑色にしていたが、オリーブの緑色、黄楊の黄緑色、樫と松の灰緑色、糸杉の黒緑色を区別できるようになった。このような目立たない鑑識力の向上は私に自然の事物を詳しく観察させ、必ずといっていいほど、形や色調を単純化しがちである記憶に疑いを抱かせるように仕向けた。
世間の生業は、神秘的な作用には全く無関係な仮借のない論理に従って進展し、そして結末がつく、というのが私の意見である。
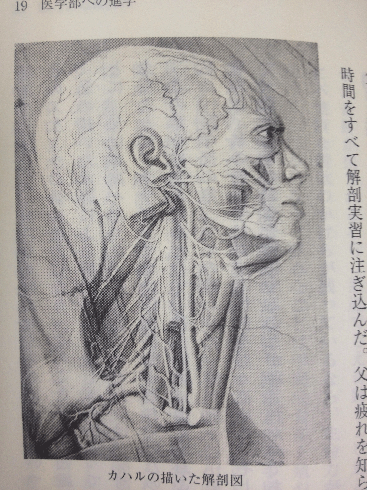
カハールは絵が大好きだったようで、それは彼のスケッチからも伺い知ることができます。写真は、彼が父親と一緒に解剖学を勉強していたときのスケッチです。
さて、最後に情報募集。カハールが下記のように紹介したファーブルの「宇宙」という本を読みたくなって探しているのですが、見つかりません。ご存知の方がいらっしゃったら御教授頂ければ幸いです。
私はラプラスの有名な著作を読もうと思って、その下準備のため、天文学に関する通俗的な本、特にフラマリオンの有名な人気のある本と、天才的な昆虫の観察者ジャン・アンリ・ファーブルの本を参考にしようと考えた。フラマリオンの数々の本は私を大いに楽しませてくれたが、知識欲を完全に満たしてはくれなかった。それらの本は豊かな叙情味、打ち解けた親しみ、華やかな文章では優れていたが、論証がほとんどなかった。それに引き替え、『宇宙』と題されたファーブルの小さな手引書は、私にとって素晴らしい天啓となった。その本には、分別と節度に貫かれた文章が躍動していた。(「昆虫の王」が優れた詩人であることは良く知られている) しかも、言葉が思想をおし殺していない。本のすべての頁にわたって、初心者に幾何学的方法―その方法の助けで、宇宙形状誌と天文学の驚くべき真理が発見された―の基本的メカニズムを手ほどきしようとする配慮が息づいていた。三角形の定義に始まり、天文学が獲得した最も優れた知見に終わるこの小冊子を読んだ私は、ついにそれまで軽蔑していた幾何学、憎んでいた三角法と和解した。宇宙空間の科学は、若干の器具の力を借りて、紙の上に何本かの線を引くことによって地球の大きさを測り、地球の実際の形を決定し、月までの距離と大きさを決め、太陽の容積と太陽までの距離を研究し、遊星の軌道と形を決定するような壮挙を成し遂げたことに気付いて、私はびっくりした。もっと卑近な仕事では、登らずに塔や山の高さや幅を知ること、渡らずに川の幅を測ること、海に沈んだ船の位置を決定すること等があった。特に、二千年以上も前にサモスのヒッパルコスによってなされた太陽までの距離に関する幾何学的な極めて巧妙な論証に、私は心から驚嘆した。今日、三角法は、太陽までの距離の割り出しや、もっと他の大きな問題の解決のために非常に正確で洗練された方法にまで高められている。しかしながら、幾何学の卓越した力を人類に明らかにしたこのギリシアの天文学者が、先駆者の一人であることを認めなければならない。